Quiz et exercices
Exercice 1 :
Soit $f$ une fonction définie et dérivable sur $ \mathbb R$. Sachant que $f'(2) = 3$ et que $f(2) = 4$, détermine l’équation de la tangente à la courbe de $f$ au point d’abscisse $x = 2$.
On sait que l’équation de la tangente à la courbe en $x= a$ est: $y = f'(a) (x-a) + f(a)$ Soit ici $y = f'(2) (x-2) + f(2)$
D’où $y = 3(x-2) +4$
Finalement $y = 3x-2$
Exercice 2 :
Soit $f$ une fonction définie et dérivable sur $\mathbb R$. Sachant que $f'(3) = -2$ et que la courbe représentative de $f$ passe par le point $A(3; 4)$ détermine l’équation de la tangente à la courbe de $f$ au point $A$.
On sait que l’équation de la tangente à la courbe en $x= a$ est: $y = f'(a) (x-a) + f(a)$ Soit ici $y = f'(3) (x-3) + f(3)$ Or la courbe représentative de $f$ passe par le point $A(3; 4)$ donc $f(3) = 4$
D’où $y = -2(x-3) +4$
Finalement $y = -2x+10$
Exercice 3 :
Soit $f$ une fonction définie et dérivable sur $\mathbb R$. La droite $(d)$ d’équation $y = -2x+8$ est tangente à la courbe représentative de $f$ au point d’abscisse $x = 3$. Détermine $f (3)$ et $f'(3)$.
On sait que l’équation de la tangente à la courbe en $x= a$ est :
$y = f'(a) (x-a) + f(a)$
Soit ici $y = f'(3) (x-3) + f(3)$
On développe: $y = f'(3)x -3 f'(3)+f(3)$
Or on a $y = -2x+8$
Par identification on en déduit que: \begin{equation} \left\{ \begin{aligned} f'(3)=-2 \\ ; -3f'(3)+f(3)=8 \end{aligned} \right. \iff \left\{ \begin{aligned} f'(3)=-2 \\ ; -3×(-2)+f(3)=8 \end{aligned} \right. \iff \left\{ \begin{aligned} f'(3)=-2 \\ f(3)=2 \end{aligned} \right. \end{equation}
Exercice 4 :
On a représenté ci-dessous la courbe représentative d’une fonction $f$ définie sur $\mathbb R$.
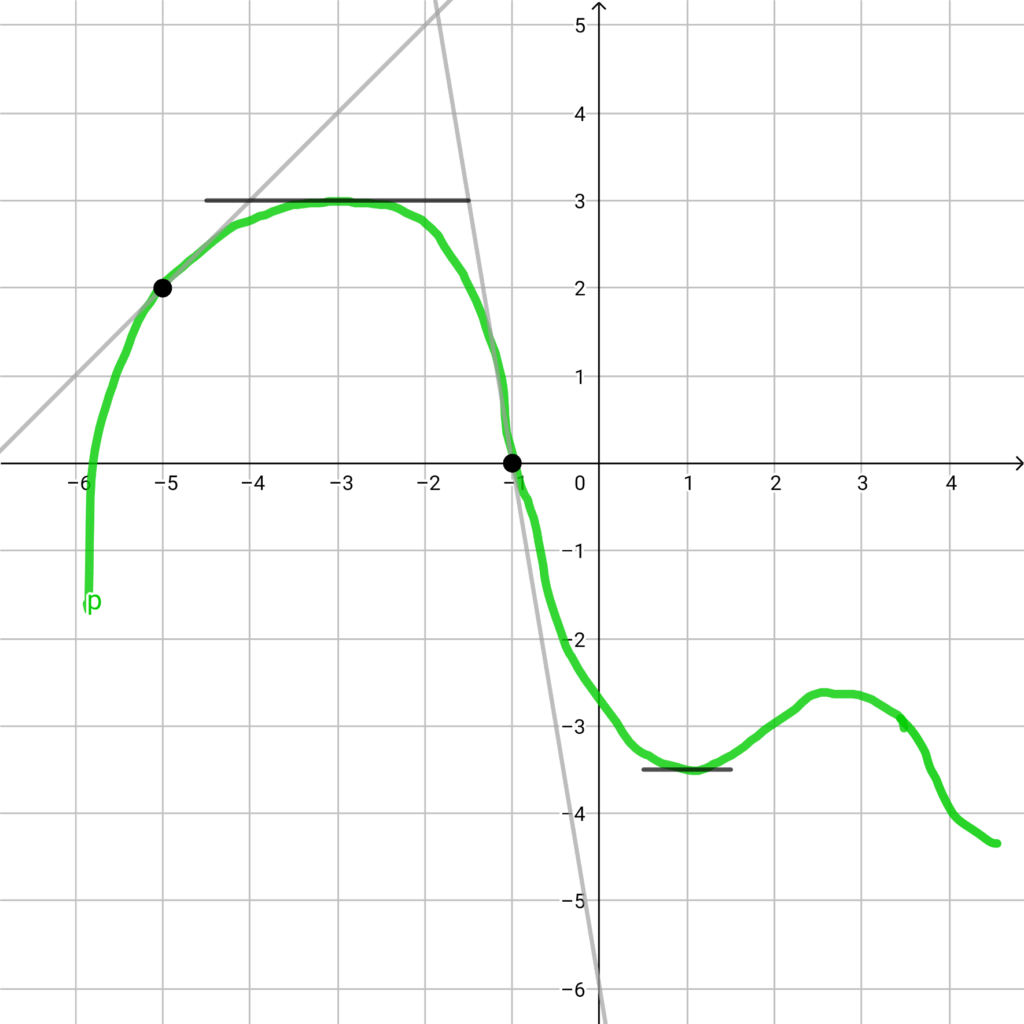
- Donner la valeur de $f'(-3)$ en justifiant puis les valeurs de $f'(-5)$, $f'(-1)$ et $f'(1)$.
- Déterminer l’équation de la tangente à la courbe de $f$ au point d’abscisse $-1$.
- On sait que $f'(3) = -1/3$. Tracer la tangente $T3$ à $C_f$ au point d’abscisse $3$.
- Le nombre dérivé en $x = -3$ est égal au coefficient directeur de la tangente en $x=-3$.
Ici la tangente est horizontale donc son coefficient directeur est nul.
D’où $f'(-3) = 0$.
On procède de même pour les autres nombres dérivés.
On en déduit donc : $f'(-5) = 1$ ; $f'(-1) = -6$ ; $f'(1) = 0$ - L’équation de la tangente à $C_f$ au point d’abscisse $x = a$ a pour expression: $y = f'(a)(x-a)+f(a)$
Ici $a = -1$
D’où $y = f'(-1)(x+1) + f(-1)$
On remplace par les valeurs: $y = -6(x+1) + 0$
Finalement: $y = -6x -6$
