EXERCICE 1
Commun à tous les candidats Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Une réponse exacte rapporte un point.Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point. Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie. Aucune justification n’est demandée.
-
On considère les suites $(u_n)$ et $(v_n)$ telles que, pour tout entier naturel $n,$
\begin{align} u_n=1-(\dfrac{1}{4}^n \text{ et } v_n=1+(\dfrac{1}{4}^n \end{align}
On considère de plus une suite $(w_n)$ qui, pour tout entier naturel $n,$ vérifie $u_n \leqslant w_n \leqslant v_n.$
On peut affirmer que :a. Les suites $(u_n)$ et $(v_n)$ sont géométriques. b. La suite $(u_n)$ est minorée par 1. c. La suite $(w_n)$ converge vers $1.$ d. La suite $(w_n)$ est croissante. -
On considère la fonction $f$ définie sur $\mathbb R$ par : $f (x) = xe^{x2}.
La fonction dérivée de $f$ est la fonction $f’$ définie sur $\mathbb R$ par:
a. $f'(x) = 2xe^{x2}.$ b. $f'(x) = (1+2x)e^{x2}.$ c. $f'(x) = (1+2x^2)e^{x2}.$ d. $f'(x) = (2+ x^2)e^{x2}.$ - Que vaut $\lim \limits_{ n \to + \infty }\dfrac{x^2-1}{2x^2-2x+1}
-
On considère une fonction $h$ continue sur l’intervalle $[−1 ; 1]$ telle que
\begin{align} h(-1)=0 \mspace{20mu} h(0)=0 \mspace{20mu} h(1)=0. \end{align} On peut affirmer que :
- La fonction $h$ est croissante sur l’intervalle $[−1 ; 0].$
- La fonction $h$ est positive sur l’intervalle $[−1 ; 1].$
- Il existe au moins un nombre réel a dans l’intervalle $[0; 1]$ tel que $h(a) = 1.$
- L’équation $h(x) = 1$ admet exactement deux solutions dans l’intervalle $[−1 ; 1].$
-
- $g$ admet un maximum en $−2.$
- $g$ est croissante sur l’intervalle $[1; 2].$
- $g$ est convexe sur l’intervalle $[1; 2].$
- $g$ admet un minimum en $0.$
EXERCICE 2
Commun à tous les candidats On considère le cube $ABCDEFGH$ de côté $1,$ le milieu $I$ de $[EF]$ et $J$ le symétrique de $E$ par rapport à $F.$ Dans tout l’exercice, l’espace est rapporté au repère orthonormé $(A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE})$-
- Par lecture graphique, donner les coordonnées des points $I$ et $J.$
- En déduire les coordonnées des vecteurs $\overrightarrow{DJ}$, $\overrightarrow{BI}$ et $\overrightarrow{BG}$
- Montrer que $\overrightarrow{DJ}$ est un vecteur normal au plan $(BGI).$
- Montrer qu’une équation cartésienne du plan $(BGI$) est $2x − y + z −2 = 0.$
-
On note d la droite passant par $F$ et orthogonale au plan $(BGI).$
- Déterminer une représentation paramétrique de la droite $d.$
- On considère le point $L$ de coordonnées $(\frac{2}{3};\frac{1}{6};\frac{5}{6})$
Montrer que $L$ est le point d’intersection de la droite $d$ et du plan $(BGI).$
-
On rappelle que le volume $V$ d’une pyramide est donné par la formule
\begin{align}V=\dfrac{1}{3} \times B \times h \end{align} où $B$ est l’aire d’une base et $h$ la hauteur associée à cette base.
- Calculer le volume de la pyramide $FBGI.$
- En déduire l’aire du triangle $BGI$
EXERCICE 3
Commun à tous les candidats Pour préparer l’examen du permis de conduire, on distingue deux types de formation:— la formation avec conduite accompagnée;
— la formation traditionnelle.
On considère un groupe de $300$ personnes venant de réussir l’examen du permis de conduire.
Dans ce groupe :
— $75$ personnes ont suivi une formation avec conduite accompagnée; parmi elles, $50$ ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
— $225$ personnes se sont présentées à l’examen suite à une formation traditionnelle; parmi elles, $100$ ont réussi l’examen à la première présentation, $75$ à la deuxième et $50$ à la troisième présentation.
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
$A$ : « la personne a suivi une formation avec conduite accompagnée »;
$R1$ : « la personne a réussi l’examen à la première présentation »;
$R2$ : « la personne a réussi l’examen à la deuxième présentation »;
$R3$ : « la personne a réussi l’examen à la troisième présentation ».
-
Modéliser la situation par un arbre pondéré.
Dans les questions suivantes, les probabilités demandées seront données sous forme d’une fraction irréductible. -
- Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation.
- Montrer que la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation est égale à $\dfrac{1}{3}.$
- La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée?
-
On note $X$ la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
Ainsi, $X = 1$ correspond à l’évènement $R1.$
- Déterminer la loi de probabilité de la variable aléatoire $X .$
- Calculer l’espérance de cette variable aléatoire. Interpréter cette valeur dans le contexte de l’exercice.
-
On choisit, successivement et de façon indépendante, $n$ personnes parmi les $300$ du groupe étudié, où $n$ est un entier naturel non nul. On assimile ce choix à un tirage avec remise de $n$ personnes parmi les $300$ personnes du groupe.
On admet que la probabilité de l’évènement $R3$ est égale à $\dfrac{1}{6}.$-
Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à $1−(\dfrac{5}{6})^n$
On considère la fonction Python seuil ci-dessous, où p est un nombre réel appartenant à l’intervalle $]0;1[.$def seuil(p)
$\qquad n = 1$
$\qquad$ while 1-(5/6)**n<=p:
$\qquad \qquad r=(2+r)/(1+r)$
$\qquad \qquad n = n+1$ $\qquad$ return $n$ - Quelle est la valeur renvoyée par la commande seuil$(0,9)$? Interpréter cette valeur dans le contexte de l’exercice.
-
Dans le contexte de cette question, préciser un évènement dont la probabilité est égale à $1−(\dfrac{5}{6})^n$
EXERCICE A
exercice au choix
Principaux domaines abordés
Logarithme
Dérivation, convexité, limites
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :Logarithme
Dérivation, convexité, limites
— la courbe représentative $C_f$ d’une fonction f définie et dérivable sur $]0 ; +∞[;$
— la tangente $T_A$ à la courbe $C_f$ au point A de coordonnées $(\dfrac{1}{e} ; e);$
— la tangente $T_B$ à la courbe $C_f$au point B de coordonnées $(1; 2).$
La droite $T_A$ est parallèle à l’axe des abscisses. La droite $T_B$ coupe l’axe des abscisses au point de coordonnées $(3; 0)$ et l’axe des ordonnées au point de coordonnées $(0; 3).$
On note $f$ la fonction dérivée de $f$
PARTIE I
- Déterminer graphiquement les valeurs de $f'(\dfrac{1}{e})$ et de $f'(1).$
- En déduire une équation de la droite $T_B$.
PARTIE II
On suppose maintenant que la fonction $f$ est définie sur $]0 ; +∞[$ par:\begin{align} f(x)= \dfrac{2+\ln (x)}{x}. \end{align}
- Par le calcul, montrer que la courbe $C_f$ passe par les points $A$ et $B$ et qu’elle coupe l’axe des abscisses en un point unique que l’on précisera.
- Déterminer la limite de $f (x)$ quand $x$ tend vers $0$ par valeurs supérieures, et la limite de $f (x)$ quand $x$ tend vers $+∞.$
- Montrer que, pour tout $x ∈]0 ; ∞[,$ \begin{align} f'(x)=\dfrac{-1-\ln (x)}{x^2}. \end{align}
- Dresser le tableau de variations de $f$ sur $]0 ; +∞[.$
- On note $f”$ la fonction dérivée seconde de $f$ On admet que, pour tout $x ∈]0 ; +∞[$ \begin{align} f”(x)=\dfrac{1+2\ln (x)}{x^3}. \end{align} Déterminer le plus grand intervalle sur lequel $f$ est convexe.
EXERCICE B
exercice au choix
Principaux domaines abordés
Équations différentielles
Fonction exponentielle; suites
Dans une boulangerie, les baguettes sortent du four à une température de $225 °C.$Équations différentielles
Fonction exponentielle; suites
On s’intéresse à l’évolution de la température d’une baguette après sa sortie du four.
On admet qu’on peut modéliser cette évolution à l’aide d’une fonction $f$ définie et dérivable sur l’intervalle $[0 ; +∞[.$
Dans cette modélisation, $f (t)$ représente la température en degré Celsius de la baguette au bout de la durée $t$, exprimée en heure, après la sortie du four.
Ainsi,$f (0,5)$ représente la température d’une baguette une demi-heure après la sortie du four.
Dans tout l’exercice, la température ambiante de la boulangerie est maintenue à $25 °C.$
On admet alors que la fonction $f$ est solution de l’équation différentielle $ y’ +6y = 150.$
-
- Préciser la valeur de $f (0)$.
- Résoudre l’équation différentielle $y’ +6y = 150.$
- En déduire que pour tout réel $t \geqslant 0$, on a $f (t) = 200e^{−6t} +25$.
- Par expérience, on observe que la température d’une baguette sortant du four:
— décroît; — tend à se stabiliser à la température ambiante. La fonction $f$ fournit-elle un modèle en accord avec ces observations? -
Montrer que l’équation $f (t) = 40$ admet une unique solution dans $[0 ; +∞[$.
Pour mettre les baguettes en rayon, le boulanger attend que leur température soit inférieure ou égale à $40 °C$. On note $T_0$ le temps d’attente minimal entre la sortie du four d’une baguette et sa mise en rayon.
On donne en page suivante la représentation graphique de la fonction $f$ dans un repère orthogonal.
- Avec la précision permise par le graphique, lire $T_0$. On donnera une valeur approchée de $T_0$ sous forme d’un nombre entier de minutes.
-
On s’intéresse ici à la diminution, minute après minute, de la température d’une baguette à sa sortie du four.
Ainsi, pour un entier naturel $n$, Dn désigne la diminution de température en degré Celsius d’une baguette entre la n-ième et la (n +1)-ième minute après sa sortie du four.
On admet que, pour tout entier naturel $n$:
\begin{align} D_n=f(\dfrac{n}{60})-f(\dfrac{n+1}{60}). \end{align}
-
Vérifier que $19$ est une valeur approchée de $D_0$ à $0,1$ près, et interpréter ce résultat dans le contexte de l’exercice.
-
Vérifier que l’on a, pour tout entier naturel $n$:
\begin{align} D_n=200e^{-0,1n}(1-e^{-0,1}) \end{align}
En déduire le sens de variation de la suite $(D_n)$, puis la limite de la suite $(D_n)$.
Ce résultat était-il prévisible dans le contexte de l’exercice?
-
Vérifier que $19$ est une valeur approchée de $D_0$ à $0,1$ près, et interpréter ce résultat dans le contexte de l’exercice.
EXERCICE 1
Commun à tous les candidats-
On considère les suites $(u_n)$ et $(v_n)$ telles que, pour tout entier naturel $n,$
\begin{align}
u_n = 1−(\dfrac{1}{4})^n \text{ et } v_n = 1+(\dfrac{1}{4})^n.
\end{align}
On considère de plus une suite $(w_n)$ qui, pour tout entier naturel _n, vérifie $u_n \leqslant w_n \leqslant v_n.$
On peut affirmer que:
b. La suite $(w_n)$ converge vers $1.$
|| Application directe du théorème dit « des gendarmes » - On considère la fonction $f$ définie sur $\mathbb R$ par: $f (x) = x e^{x^2}. La fonction dérivée de $f$ est la fonction $f’$ définie sur $\mathbb R$ par: c. $f'(x) = (1+2x^2)e^{x^2}.$ ||$f'(x) = 1× e^{x^2} + x ×2x e^{x^2} = (1+2x^2) e^{x^2}$
- Que vaut $\lim \limits_{ n \to + \infty } \dfrac{x^2-1}{2x^2-2x+1}$ c. $\dfrac{1}{2}.$ $\bigg\rVert\lim \limits_{ n \to + \infty } \dfrac{x^2-1}{2x^2-2x+1}= \lim \limits_{ n \to + \infty } \dfrac {x^2(1-\frac{1}{x^2})} {x^2(2-\frac {2}{x}+\frac{1}{x^2})}=\lim \limits_{ n \to + \infty } \dfrac{1-\frac{1}{x^2}}{2-\frac{2}{x}+\frac{1}{x^2}}=\dfrac{1}{2}$
-
On considère une fonction $h$ continue sur l’intervalle $[−1 ; 1]$ telle que
$h(−1) = 0 \mspace{40mu} h(0) = 2 \mspace{40mu} h(1) = 0.$ On peut affirmer que : c. Il existe au moins un nombre réel a dans l’intervalle $[0; 1]$ tel que $h(a) = 1.$ || Application du théorème des valeurs intermédiaires sur l’intervalle $[0 ; 1].$ - On suppose que g est une fonction dérivable sur l’intervalle $[−4 ; 4].$ On donne ci-contre la représentation graphique de sa fonction dérivée $g’.$ On peut affirmer que: c.$g$ est convexe sur l’intervalle $[1; 2].$ $\bigg\rVert \text{ La fonction } g’ \text{ est croissante sur l’intervalle } [1 ; 2], \text{ donc la fonction } g \text{ est convexe sur cet intervalle.}$
EXERCICE 2
Commun à tous les candidats On considère le cube $ABCDEFGH$ de côté $1$, le milieu $I$ de $[EF]$ et $J$ le symétrique de $E$ par rapport à $F.$ Dans tout l’exercice, l’espace est rapporté au repère orthonormé $(A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE})$ Les sommets du cube ont pour coordonnées : $A\begin{pmatrix} 0 \\ 0 \\ 0\end{pmatrix},B\begin{pmatrix} 1 \\ 0 \\ 0\end{pmatrix},C\begin{pmatrix} 0 \\ 1 \\ 0\end{pmatrix},E\begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix},C\begin{pmatrix} 1 \\ 1 \\ 0\end{pmatrix},F\begin{pmatrix} 1 \\0 \\ 1\end{pmatrix},H\begin{pmatrix} 0 \\ 1 \\ 1\end{pmatrix},\text{ et }G\begin{pmatrix} 1 \\ 1 \\ 1\end{pmatrix}.$-
-
• Le point $I$ est le milieu de $[EF]$ donc $I$ a pour coordonnées $\begin{pmatrix} \frac{1}{2} \\0 \\ 1\end{pmatrix}$
Le point $J$ est le symétrique de $E$ par rapport à $F,$ donc $J$ a pour coordonnées $\begin{pmatrix} 2 \\0 \\ 1\end{pmatrix}$ - On en déduit les coordonnées des vecteurs $\overrightarrow{DJ}\begin{pmatrix} 2 \\-1 \\ 1\end{pmatrix},\overrightarrow{BI}\begin{pmatrix} \frac{1}{2} \\0 \\ 1\end{pmatrix} \text { et } \overrightarrow{BJ}\begin{pmatrix} 0 \\1 \\ 1\end{pmatrix}$
-
• Les vecteurs $\overrightarrow{BI}$ et $\overrightarrow{BG}$ ne sont pas colinéaires donc ce sont deux vecteurs directeurs du plan $(BGI).$
• $\overrightarrow{DJ} . \overrightarrow{BI}=-1+0+1=0$ donc $\overrightarrow{DJ} \bot \overrightarrow{BI}$
• $\overrightarrow{DJ} . \overrightarrow{BG}=0-1+1=0$ donc $\overrightarrow{DJ} \bot \overrightarrow{BG}$
Donc le vecteur $\overrightarrow{DJ}$ est orthogonal à deux vecteurs non colinéaires du plan $(BGI),$ donc il est normal au plan $(BGI).$ -
• Le vecteur $\overrightarrow{DJ}\begin{pmatrix} 2 \\-1 \\ 1\end{pmatrix}$ est normal au plan $(BGI)$ donc le plan $(BGI)$ a une équation de la forme $2x − y + z + d = 0.$
• Le point $B$ appartient au plan $(BGI)$ donc les coordonnées de $B$ vérifient l’équation du plan donc: $ 2x_B − y_B + z_B + d = 0$, ce qui équivaut à $2−0+0+ d = 0$, ce qui veut dire que $d = −2.$ Donc une équation cartésienne du plan $(BGI)$ est $2x − y + z −2 = 0.$
-
• Le point $I$ est le milieu de $[EF]$ donc $I$ a pour coordonnées $\begin{pmatrix} \frac{1}{2} \\0 \\ 1\end{pmatrix}$
-
On note $d$ la droite passant par $F$ et orthogonale au plan $(BGI).$
-
La droite $d$ est orthogonale au plan $(BGI),$ et $\overrightarrow{DJ}$ est un vecteur normal au plan $(BGI),$ donc $\overrightarrow{DJ}$ est un vecteur directeur de la droite $d.$
Le point $F$ appartient à la droite $d$ donc la droite $d$ est l’ensemble des points $M$ de coordonnées $(x ; y ; z)$ tels que $\overrightarrow{FM}$ et $\overrightarrow{DJ}$ soient colinéaires.
$\overrightarrow{FM}$ et $\overrightarrow{DJ}$ colinéaire $ \iff \overrightarrow{FM} =t. \overrightarrow{DJ} \iff \begin{cases} x −1 = t ×2 \\ y −0 = t ×(−1) \\ z −1 = t ×1 \end{cases}$
Donc la droite $d$ a pour équation $\begin{align} \begin{cases} x = 1 +2t \\ y =- t \\ z= t +1 \end{cases} ,t \in \mathbb R \end{align}$
-
On considère le point $L$ de coordonnées $(\frac{2}{3};\frac{1}{6};\frac{5}{6})$
• Pour prouver que $L ∈ d$, on cherche $t$ pour que $\begin{cases} \frac{2}{3}=1+2t \\ \frac{1}{6}=-t \\ \frac{5}{6}=1+t \end{cases}$
On trouve $t = −\dfrac{1}{6}$ donc $L ∈ d.$
• Le plan $(BGI)$ a pour équation $2x − y +z −2 = 0$; or $2x_L − y_L +z_L −2 =\dfrac{4}{3}-\dfrac{1}{6}+\dfrac{5}{6} = 0$, donc $L ∈ (BGI).$
Le point $L$ est donc le point d’intersection de la droite $d$ et du plan $(BGI).$
-
La droite $d$ est orthogonale au plan $(BGI),$ et $\overrightarrow{DJ}$ est un vecteur normal au plan $(BGI),$ donc $\overrightarrow{DJ}$ est un vecteur directeur de la droite $d.$
-
-
La pyramide $FBGI$ a pour base le triangle rectangle $FBG,$ et pour hauteur $IF.$
• $IF =\dfrac{1}{2}$
• Le triangle rectangle $FBG$ a pour aire $\dfrac{FG \times FB}{2}=\dfrac{1}{2}.$
Le volume de la pyramide $FBGI$ est donc $V=\dfrac{1}{3} \times \dfrac{1}{2} \times \dfrac{1}{2}=\dfrac{1}{12}$ -
La droite $d$ est orthogonale au plan $(BGI)$ et coupe ce plan en $L.$ Le point $F$ appartient à la droite $d,$ donc on peut dire que la distance $FL$ est la distance du point $F$ au plan $(BGI),$ autrement dit c’est la hauteur de la pyramide $FBGI$ dont le triangle $BGI$ est la base.
$FL^2=(\frac{2}{3}-1)^2+(\frac{1}{6}-0)^2+(\frac{5}{6}-1)^2=\dfrac{1}{9}+\dfrac{1}{36}+\dfrac{1}{36}=\dfrac{6}{36}=\dfrac{1}{6}$ donc $FL=\dfrac{1}{\sqrt 6}$
On appelle $A$ l’aire du triangle $BGI.$ On exprime le volume de la pyramide $FBGI :$
$V=\frac{1}{3} \times FL \times A \iff \frac{1}{12}=\frac{1}{3}\times \frac{1}{\sqrt 6} \times A \iff \frac{3 \times \sqrt 6}{12}=A \iff A=\frac{\sqrt 6}{4}$
L’aire du triangle BGI est égale à $\dfrac{\sqrt 6}{4}$
-
La pyramide $FBGI$ a pour base le triangle rectangle $FBG,$ et pour hauteur $IF.$
• $IF =\dfrac{1}{2}$
EXERCICE 3
Commun à tous les candidats Pour préparer l’examen du permis de conduire, on distingue deux types de formation : — la formation avec conduite accompagnée; — la formation traditionnelle. On considère un groupe de $300$ personnes venant de réussir l’examen du permis de conduire. Dans ce groupe: — $75$ personnes ont suivi une formation avec conduite accompagnée; parmi elles, $50$ ont réussi l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation. — $225$ personnes se sont présentées à l’examen suite à une formation traditionnelle; parmi elles, $100$ ont réussi l’examen à la première présentation, $75$ à la deuxième et $50$ à la troisième présentation. On interroge au hasard une personne du groupe considéré. On considère les évènements suivants : A : « la personne a suivi une formation avec conduite accompagnée »; R1 : « la personne a réussi l’examen à la première présentation »; R2 : « la personne a réussi l’examen à la deuxième présentation »; R3 : « la personne a réussi l’examen à la troisième présentation ».- On modélise la situation par un arbre pondéré.
-
-
La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation est:
$P (A ∩ R_2) = P(A)× P_A (R_2) =\dfrac{75}{300} \times \dfrac{25}{75}=\dfrac{25}{300}=\dfrac{1}{12}.$ -
La probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation est égale à $P (R_2)..$
D’après la formule des probabilités totales:
$P (R_2) = P (A ∩ R_2)+ P (\overline{A} ∩ R_2)=\dfrac{25}{300} + \dfrac{125}{300}\times \dfrac{75}{125} =\dfrac{25}{300} + \dfrac{75}{300}=\dfrac{1}{3}.$ -
La personne interrogée a réussi l’examen à sa deuxième présentation. La probabilité qu’elle ait suivi une formation avec conduite accompagnée est:
$P_{R_2}(A) = \dfrac{P (A ∩ R_2)}{P (R_2)}=\dfrac{\frac{1}{12}}{\frac{1}{3}}=\dfrac{3}{12}=\dfrac{1}{4}.$
-
La probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation est:
-
On note $X$ la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
Ainsi, $X = 1$ correspond à l’évènement $R1.$- La loi de probabilité de la variable aléatoire $X$ est:
-
L’espérance de cette variable aléatoire est: $E(X ) = \sum{(x_i × p_i)} = 1×\dfrac{1}{2}+2×\dfrac{1}{3}+3×\dfrac{1}{6}=\dfrac{5}{3} \approx 1,67.$
Cela veut dire que le nombre de passages pour réussir l’examen est en moyenne de $1,67.$
• $P (R_1) = P (A ∩ R_1)+ P (\overline{A} ∩ R_1) =\dfrac{75}{300} \times \dfrac{50}{75} + \dfrac{255}{300}\times \dfrac{100}{255} =\dfrac{50}{300} + \dfrac{100}{300}=\dfrac{150}{300}=\dfrac{1}{2}.$$x_i$ $1$ $2$ $3$ $p_i = P(X = x_i )$ $P(R_1)$ $P(R_2)$ $P(R_3)$
• $P (R_2)=\dfrac{1}{3}$
• $P (R_3) = P (A ∩ R_3)+ P (\overline{A} ∩ R_3) =0+\dfrac{255}{300} \times \dfrac{50}{255} =\dfrac{50}{300}=\dfrac{1}{6}.$
Donc la loi de $p$
$x_i$ $1$ $2$ $3$ $p_i = P(X = x_i )$ $\dfrac{1}{2}$ $\dfrac{1}{3}$ $\dfrac{1}{6}$ -
On choisit, successivement et de façon indépendante, $n$ personnes parmi les $300$ du groupe étudié, où $n$ est un entier naturel non nul. On assimile ce choix à un tirage avec remise de $n$ personnes parmi les $300$ personnes du groupe.
On admet que la probabilité de l’évènement $R_3$ est égale à $\dfrac{1}{6}.$-
On cherche un évènement dont la probabilité est égale à $1−(\frac{5}{6})^n.$
$P(R_3) = \dfrac{1}{6}$ donc $P(\overline{R_3}) = 1 − \dfrac{1}{6} = \dfrac{5}{6}.$ Le nombre 56 est donc la probabilité de l’événement « $R1$ ou $R2$ », c’est-à-dire la probabilité qu’une personne prise au hasard réussisse l’examen à la première tentative ou à la deuxième.
La probabilité que $n$ personnes réussissent l’examen à la première ou à la deuxième tentative est de $(\dfrac{5}{6})^n.$
L’événement de probabilité $1-(\dfrac{5}{6})^n.$ est l’événement contraire du précédent, donc correspond à l’événement « au moins une personne n’a pas réussi l’examen à la première ou à la deuxième tentative », c’est-à-dire « au moins une personne a réussi l’examen à la troisième tentative ».
On considère la fonction Python seuil ci-dessous, où $p$ est un nombre réel appartenant à l’intervalle $]0;1[.$def seuil()
$\qquad n = 1$
$\qquad$ while 1-(5/6)**n:
$\qquad \qquad r=(2+r)/(1+r)$
$\qquad \qquad n = n+1$ $\qquad$ return $n$ -
La valeur renvoyée par seuil$(0.9)$ est la première valeur de n pour laquelle $1-(\dfrac{5}{6})^n > 0,9.$
On résout cette inéquation:
$1-(\frac{5}{6})^n > 0,9$
$\iff 0,1>(\frac{5}{6})^n $
$\iff \ln (0,1)> \ln((\frac{5}{6})^n) $
$\iff \ln (0,1)> n\ln(\frac{5}{6}) $
$\iff \dfrac{\ln(0,1)}{\ln(\frac{5}{6})} < n\dfrac{\ln (0,1)}{(\frac{5}{6})} \approx 12,6$ donc la commande seuil$(0.9)$ renvoie la valeur $13.$
Il faut donc prendre $n = 13$ personnes sur les $300$ pour que la probabilité d’en avoir une qui a réussi l’examen à sa troisième tentative soit supérieure à $0,9.$
-
On cherche un évènement dont la probabilité est égale à $1−(\frac{5}{6})^n.$
EXERCICE A
exercice au choix
Principaux domaines abordés
Logarithme
Dérivation, convexité, limites
Sur le graphique ci-dessous, on a représenté dans un repère orthonormé :
• la courbe représentative $C_f$ d’une fonction $f$ définie et dérivable sur $]0 ; +∞[;$
• la tangente TA à la courbe $C_f$ au point A de coordonnées $(\dfrac{1}{r} ; e);$
• la tangente $T_B$ à la courbe $C_f$ au point $B$ de coordonnées $(1; 2).$
La droite $T_A$ est parallèle à l’axe des abscisses. La droite $T_B$ coupe l’axe des abscisses au point de coordonnées $(3; 0)$ et l’axe des ordonnées au point de coordonnées $(0; 3).$
On note $f’$ la fonction dérivée de $f$
PARTIE I
Logarithme
Dérivation, convexité, limites
- • La droite $T_A$ est tangente à la courbe $C_f$ au point $A$ de coordonnées $(\dfrac{1}{e} ; e)$; elle a donc comme coefficient directeur $f'(\dfrac{1}{e})$. La droite $T_A$ est parallèle à l’axe des abscisses donc son coefficient directeur est nul. On peut donc déduire que $f'(\dfrac{1}{e})=0.$ • La droite $T_B$ est tangente à la courbe $C_f$ au point $B$ de coordonnées $(1; 2),$ donc elle a pour coefficient directeur $f'(1).$ La droite $T_B$ coupe l’axe des abscisses au point de coordonnées $(3; 0)$ et l’axe des ordonnées au point de coordonnées $(0; 3),$ donc on peut en déduire que son coefficient directeur est $\dfrac{3-0}{0-3}=1$ On a donc $f'(1) = −1.$
- La droite $T_B$ a pour coefficient directeur $−1$ et $3$ pour ordonnée à l’origine, donc elle a pour équation: $y = −x +3.$
-
• $f(\frac{1}{e})= \dfrac{2+\ln(\frac{1}{e})}{\frac{1}{e}}= e (2−\ln(e)) == e (2−1) = e$ donc $A ∈ C_f$
• $f (1) = \dfrac{2+\ln(1)}{1}=2$ donc $B ∈ C_f.$
• La courbe $C_f$ coupe l’axe des abscisses en un point dont l’abscisse est solution de l’équation $f (x) = 0.$ On résout dans $]0 ; +∞[$ cette équation.
$f(x)=0 \iff \dfrac{2+\ln(1)}{1}=0 \iff 2+\ln(x)=0 \iff \ln(x)=-2 \iff x=e{-2}$ • Donc la courbe $C_f$ coupe l’axe des abscisses en un point unique de coordonnées $(e^{−2} ; 0).$ - Calculs des limites. \begin{align} \left. \begin{array}{ll} \lim\limits_{\substack{x \rightarrow 0 \\ x>0}}(2+ln(x)) = −∞ \\ \lim\limits_{\substack{x \rightarrow 0 \\ x>0}}= +∞ \end{array} \right \}\iff = \lim\limits_{\substack{x \rightarrow 0 \\ x>0}}(2+ln(x))\times \dfrac{1}{x}=−∞ \text{ donc } \lim\limits_{\substack{x \rightarrow 0 \\ x>0}}f(x)=0 \end{align} \begin{align} \left. \begin{array}{ll} \lim \limits_{ n \to + \infty }\dfrac{2}{x} = 0 \\ \lim \limits_{ n \to + \infty }\dfrac{\ln(x)}{x}= 0 \end{array} \right \}\iff = \lim \limits_{ n \to + \infty } \dfrac{2}{x} +\dfrac{\ln(x)}{x}=0 \text{ donc } \lim \limits_{ n \to + \infty }f(x)=0 \end{align}
-
Pour $x ∈]0 ; ∞[$
$ f'(x) =\dfrac{\frac{1}{x}\times x–(2+ \ln (x))\times 1}{x^2}=\dfrac{1-2-\ln(x)}{x^2}=\dfrac{-1-\ln(x)}{x^2}.$ -
$f'(x)$ est du signe de $−1−\ln(x)$; $−1−\ln(x) > 0 \iff −1 > \ln(x) \iff x < e^{−1}$
On dresse le tableau de variations de $f$ sur $]0 ; +∞[ :$ -
On admet que, pour tout $x ∈]0 ; +∞[, f”(x) =\dfrac{1+2\ln(x)}{x^3}$
La fonction $f$ est convexe sur les intervalles sur lesquels $f”$ est positive.
Sur $]0 ; +∞, x3 > 0$ donc $f”(x) \geqslant 0 \iff \dfrac{1+2\ln(x)}{x^3} \geqslant 0 \iff 1+2\ln(x) \geqslant 0 \iff \ln(x) \geqslant −\dfrac{1}{2} \iff \geqslant e^{-\frac{1}{2}}$
Donc le plus grand intervalle sur lequel la fonction $f$ est convexe est $[e^{-\frac{1}{2}} ; +∞[$.
EXERCICE B
exercice au choix
Principaux domaines abordés
Équations différentielles
Fonction exponentielle; suites
Dans une boulangerie, les baguettes sortent du four à une température de $225 °C.$
On s’intéresse à l’évolution de la température d’une baguette après sa sortie du four.
On admet qu’on peut modéliser cette évolution à l’aide d’une fonction $f$ définie et dérivable sur l’intervalle $[0 ; +∞[.$
Dans cette modélisation, $f (t)$ représente la température en degré Celsius de la baguette au bout de la durée $t$, exprimée en heure, après la sortie du four.
Ainsi, $f (0,5)$ représente la température d’une baguette une demi-heure après la sortie du four.
Dans tout l’exercice, la température ambiante de la boulangerie est maintenue à $25 °C.$
On admet alors que la fonction $f$ est solution de l’équation différentielle $y’ +6y = 150.$
Équations différentielles
Fonction exponentielle; suites
-
- $f (0)$ représente la température d’une baguette lors de sa sortie du four, c’est-à-dire $225 ◦C$
- Pour résoudre l’équation, on la met sous la forme $y’ = ay +b$ avec $a$ et $b$ des réels. On obtient:
$y’= −6y +150 \iff y’= ay + b$ avec $ \left \{ \begin{align} a =-6 \\b=150\end{align}\right.$
On sait alors que les solutions de cette équation sont toutes les fonctions de la forme:
\begin{align} f (t) = − \dfrac{b}{a}+C e^{at}, C ∈ \mathbb R \end{align} Les solutions de l’équation différentielle sont donc toutes les fonctions de la forme: \begin{align} f (t) = − \dfrac{150}{-6}+C e^{-6t} \\ f (t) = − 25+C e^{-6t} \end{align} - La solution de l’équation différentielle a été obtenue en question $b$. Il reste à exploiter la condition initiale $f (t = 0) = f (0) = 225$ d’après la valeur trouvée à la question a. La fonction qui satisfait donc le modèle de l’exercice est la solution de l’équation: \begin{align}f (0) = 225 \iff C e^0 +25 = 225 \iff C +25 = 22 \iff C = 200\end{align} Donc on a bien, pour tout réel $t \geqslant 0 :$ \begin{align} f (t) = 200e^{-6t} +25 \end{align}
-
Par expérience, on observe que la température d’une baguette sortant du four décroît et tend à se stabiliser à la température ambiante.
— Vérifions d’abord que la fonction $f$ décroît. $f$ est d’abord bien dérivable pour tout réel $t \geqslant 0$ comme composée de fonctions dérivables et:
pour tout réel $t \geqslant 0, f'(t) = −1200e^{−6t}$
Or, pour tout réel $t \geqslant 0 :$
$\left \{
\begin{align}
e^{−6t} >0\\
-1200<0
\end{align} \Rightarrow f'(t) < 0 \Rightarrow \text{ est bien décroissante (strictement)}
\right.$
— Pour vérifier que la température tend à se stabiliser à la température ambiante $(25 ◦C),$ nous allons calculer la limite de la fonction $f$ en $+∞ :$
$\lim \limits_{ t \to + \infty }e^{−6t}=0 \underset{\text{par produit}} \iff \lim \limits_{ t \to + \infty }200e^{−6t}=0 \underset{\text{par somme}} \iff \lim \limits_{ t \to + \infty }200e^{−6t}+25=25=\lim \limits_{ t \to + \infty }f(t) $
La fonction $f ,$ qui représente la température de la baguette (en $◦C$) au bout du temps, a pour limite $25$ en $+∞.$ Cela signifie donc bien que la température tend à se stabiliser à la température ambiante de $25 ◦C.$
Donc la fonction $f$ fournit un modèle en accord avec ces observations -
La fonction $f$ est continue et décroissante strictement donc monotone sur $[0 : +∞[.$ Par ailleurs, $f (0) = 225$ et $\lim \limits_{ n \to + \infty }f (t) = 25$ donc, d’après le théorème des valeurs intermédiaires, il existe un unique élément $c ∈ [0;+∞[ tel que f (c) = 40.$
Pour mettre les baguettes en rayon, le boulanger attend que leur température soit inférieure ou égale à $40 °C.$ On note $T_0$ le temps d’attente minimal entre la sortie du four d’une baguette et sa mise en rayon.
On donne la représentation graphique de la fonction $f$ dans un repère orthogonal. - La courbe $C_f$ semble atteindre $40$ vers $0,43$ heure soit $0,43×60 = 25,8$ minutes. On trouve donc une valeur approchée de $26$ minutes.
-
On s’intéresse ici à la diminution, minute après minute, de la température d’une baguette à sa sortie du four.
Ainsi, pour un entier naturel $n,$ Dn désigne la diminution de température en degré Celsius d’une baguette entre la n-ième et la (n +1)-ième minute après sa sortie du four.
On admet que, pour tout entier naturel $n : D_n = f(\dfrac{n}{60})=f(\dfrac{n+1}{60}).$-
On cherche une valeur approchée de $D_0.$
$\begin{align} D_0 = f(\dfrac{0}{60})-f(\dfrac{1}{60}). \\ =f(0)-f(\dfrac{1}{60}) \\ 200e^0+\cancel{25}-(200e^{-\frac{6}{60}}+\cancel{25})\\ =200-200e{-\frac{6}{60}}\\ \approx 19,03 \end{align}$
Donc $19$ est bien une valeur approchée de $D_0$ à $0,1$ près. Cela signifie que la diminution de température qui se fait lors de la première minute après la sortie du four est d’environ $19 ◦C.$
Au bout d’une minute, la baguette est donc à $225−19 = 206 ◦C.$
- .
$D_n = f(\dfrac{n}{60})-f(\dfrac{n+1}{60}). $
$=200e^{-6\times \frac{n}{60}}+cancel{25}-(200e^{-6\times \frac{n+1}{60}}+25) $
$=200e^{-0,1n}-200e^{\frac{-6n}{60}+(\frac{-6}{60})}$
$=200e^{-0,1n}-200e^{-0,1n}-e^{-0,1}$
$D_n=200e^{-0,1n}(1-200e^{-0,1}-)$
Pour étudier le sens de variation de la suite $(D_n)$, on étudie le signe de $D_{n+1} − D_n.$ Pour tout entier naturel $n :$
$D_{n+1} − D_n = 200e^{-0,1(n+1)}(1− e^{-0,1})−200e^{-0,1n} (1− e^{-0,1}) $
$= 200^{-0,1n} × e^{-0,1}(1− e^{-0,1})−200e^{-0,1n} (1− e^{-0,1}) $
$D_{n+1} − D_n = 200e^{-0,1n} (1− e^{-0,1})[e^{-0,1} −1]$
Étudions le signe de cette expression pour tout entier naturel $n :$ $\left \{ \begin{align} 200e^{−0,1n} \geqslant 0 \\ 1-e^{−0,1} \geqslant 0 \\ e^{−0,1}-1 \leqslant 0 \end{align} \underset{\text{par produit}}\iff D_{n+1} −D_n \leqslant 0 \Rightarrow\text{ la suite }(D_n) \text{ est décroissante.} \right.$
Calculons alors la limite de cette suite :
$\left \{ \begin{align} \lim \limits_{ n \to + \infty } 200e^{−0,1n} = 0 \\ \lim \limits_{ n \to + \infty } 1-e^{−0,1} =1-e^{−0,1} \\ \lim \limits_{ n \to + \infty } e^{−0,1}-1 =e^{−0,1}-1 \end{align} \underset{\text{par produit}}\iff \lim \limits_{ n \to + \infty D_n =0} \right.$
Nous trouvons une limite de $0$ pour $D_n.$ Puisque la baguette tend à se stabiliser à la température ambiante, la diminution de température entre la n-ième et la $(n + 1)$-ième minute va tendre vers $0.$ Le résultat était bien prévisible dans le contexte de l’exercice.
-
On cherche une valeur approchée de $D_0.$
Les probabilités demandées dans cet exercice seront arrondies à $10^{-3}$
Un laboratoire pharmaceutique vient d’élaborer un nouveau test anti-dopage.
Partie A
Voir la correctionUne étude sur ce nouveau test donne les résultats suivants :
- si un athlète est dopé, la probabilité que le résultat du test soit positif est $0,98$ (sensibilité du test);
- si un athlète n’est pas dopé, la probabilité que le résultat du test soit négatif est $0,995$ (spécificité du test).
On note D l’évènement « l’athlète est dopé » et $T$ l’évènement « le test est positif». On admet que la probabilité de l’évènement $D$ est égale à $0,08$.
- Traduire la situation sous la forme d’un arbre pondéré.
- Démontrer que $P(T ) = 0,083$.
-
- Sachant qu’un athlète présente un test positif, quelle est la probabilité qu’il soit dopé?
- Le laboratoire décide de commercialiser le test si la probabilité de l’évènement « un athlète présentant un test positif est dopé » est supérieure ou égale à $0,95$. Le test proposé par le laboratoire sera-t-il commercialisé? Justifier.
Partie B
Voir la correctionDans une compétition sportive, on admet que la probabilité qu’un athlète contrôlé présente un test positif est $0,103$.
- Dans cette question $1$. on suppose que les organisateurs décident de contrôler $5$ athlètes au hasard parmi les athlètes de cette compétition.
On note $X$ la variable aléatoire égale au nombre d’athlètes présentant un test positif parmi les $5$ athlètes contrôlés.- Donner la loi suivie par la variable aléatoire $X$ . Préciser ses paramètres.
- Calculer l’espérance $E(X)$ et interpréter le résultat dans le contexte de l’exercice.
- Quelle est la probabilité qu’au moins un des $5$ athlètes contrôlés présente un test positif?
- Combien d’athlètes faut-il contrôler au minimum pour que la probabilité de l’évènement « au moins un athlète contrôlé présente un test positif » soit supérieure ou égale à $0,75$? Justifier.
Correction
Partie A
Revoir l’énoncé-
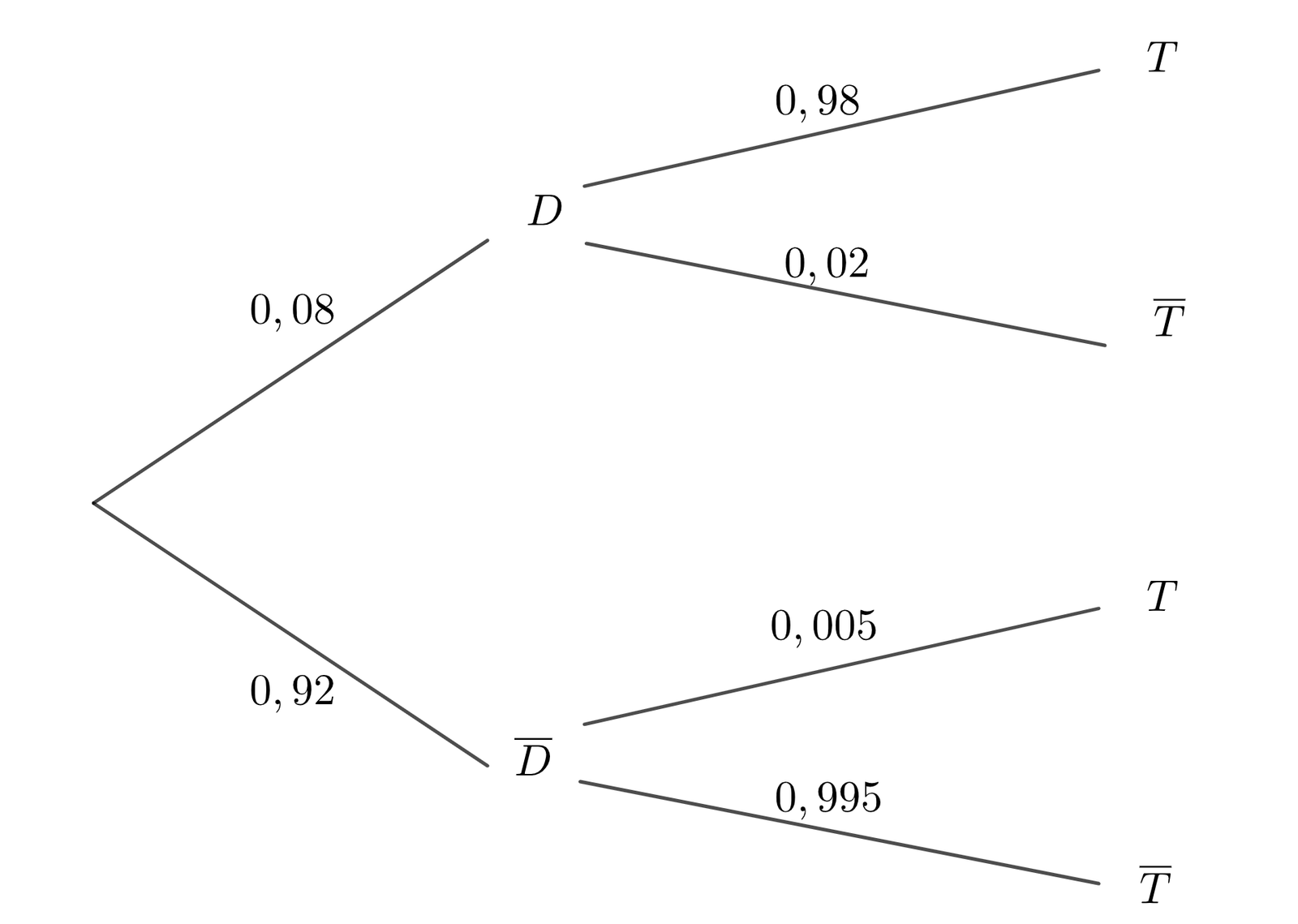
- D’après la loi des probabilités totales :
$P(T ) = P(D ∩ T )+ P(\overline{D} ∩ T)$
Or, $P(D ∩ T ) = P(D)× P_{D}(T ) = 0,08×0,98 = 0,0784$ et
$P(\overline{D} ∩ T) = P(\overline{D}) = P_{\overline{D}}(T) = 0,92×0,005 = 0,00460$. Donc : $P(T ) = 0,0784+0,0046 = 0,083$. -
- La probabilité conditionnelle $P_{(T)}(D)=\dfrac {P(T ∩ D)}{P(T)} = \dfrac {P(D ∩ T)}{P(T)}=\dfrac {0,0784}{0,083} \approx 0,9445,$ soit 0,945 au millième près
- D’après la question précédente $0,945 < 0,95$, donc le test ne sera pas commercialisé.
-
- Quel que soit l’athlète choisi la probabilité que cet athlète présente un test positif est $0,103$. La variable aléatoire $X$ suit donc une loi binomiale de paramètres $n = 5$ et $p = 0,103$.
- On sait que $E = n × p = 5×0,103 = 0,515$ : ceci montre que sur un grand nombre de contrôles, il y aura à peu près $1$ athlète sur $10$ contrôlé positif.
-
La probabilité qu’aucun athlète ne soit contrôlé positif est:
$0,1030 ×(1−0,103)5 = 0,8975 \approx 0,5807$ soit environ $0,581$ au millième près.
Donc la probabilité qu’au moins un des 5 athlètes contrôlés présente un test positif est:
$1−0,581$, soit $0,419$ au millième près.
-
On a pour n athlètes contrôlés, $P(X = 0) = 0,103^0 ×0,897^n = 0,897^n$.
Il faut donc trouver n tel que :
$1−0,897^n > 0,75 \iff 1−0,75 > 0,897^n \iff 0,25 > 0,897^n$.
La calculatrice donne le plus petit $n \in N$ vérifiant cette inéquation : pour $n = 13$, on a $0,89713 \approx 0,243$.
Il faut donc contrôler 13 athlètes en moyenne pour en trouver un positif.