Amérique du Nord – Mai 2021
Le candidat traite 4 exercices : les exercices 1, 2 et 3 communs à tous les candidats et un seul des deux exercices A et B.

Les probabilités demandées dans cet exercice seront arrondies à $10^{-3}$
Un laboratoire pharmaceutique vient d’élaborer un nouveau test anti-dopage.
Partie A
Une étude sur ce nouveau test donne les résultats suivants :
- si un athlète est dopé, la probabilité que le résultat du test soit positif est $0,98$ (sensibilité du test);
- si un athlète n’est pas dopé, la probabilité que le résultat du test soit négatif est $0,995$ (spécificité du test).
On note D l’évènement « l’athlète est dopé » et $T$ l’évènement « le test est positif». On admet que la probabilité de l’évènement $D$ est égale à $0,08$.
- Traduire la situation sous la forme d’un arbre pondéré.
- Démontrer que $P(T ) = 0,083$.
-
- Sachant qu’un athlète présente un test positif, quelle est la probabilité qu’il soit dopé?
- Le laboratoire décide de commercialiser le test si la probabilité de l’évènement « un athlète présentant un test positif est dopé » est supérieure ou égale à $0,95$. Le test proposé par le laboratoire sera-t-il commercialisé? Justifier.
Partie B
Dans une compétition sportive, on admet que la probabilité qu’un athlète contrôlé présente un test positif est $0,103$.
- Dans cette question $1$. on suppose que les organisateurs décident de contrôler $5$ athlètes au hasard parmi les athlètes de cette compétition.
On note $X$ la variable aléatoire égale au nombre d’athlètes présentant un test positif parmi les $5$ athlètes contrôlés.- Donner la loi suivie par la variable aléatoire $X$ . Préciser ses paramètres.
- Calculer l’espérance $E(X)$ et interpréter le résultat dans le contexte de l’exercice.
- Quelle est la probabilité qu’au moins un des $5$ athlètes contrôlés présente un test positif?
- Combien d’athlètes faut-il contrôler au minimum pour que la probabilité de l’évènement « au moins un athlète contrôlé présente un test positif » soit supérieure ou égale à $0,75$? Justifier.
Partie A
Revoir l’énoncé-
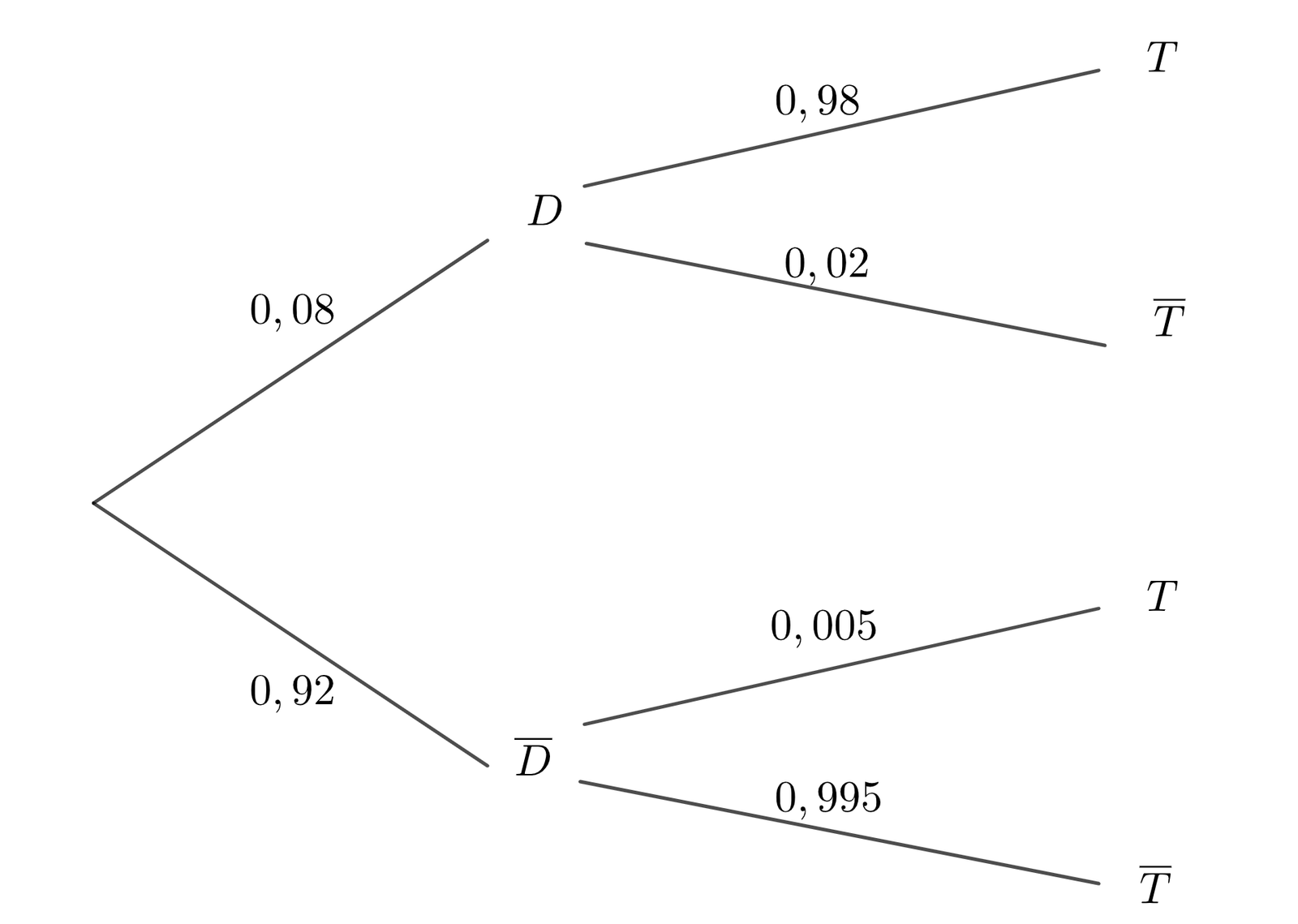
- D’après la loi des probabilités totales :
$P(T ) = P(D ∩ T )+ P(\overline{D} ∩ T)$
Or, $P(D ∩ T ) = P(D)× P_{D}(T ) = 0,08×0,98 = 0,0784$ et
$P(\overline{D} ∩ T) = P(\overline{D}) = P_{\overline{D}}(T) = 0,92×0,005 = 0,00460$.
Donc : $P(T) = 0,0784+0,0046 = 0,083$. -
- La probabilité que l’athlète soit dopé sachant que son test est positif s’écrit comme la probabilité conditionnelle suivante : $P_{T}(D)=\dfrac {P(T ∩ D)}{P(T)} = \dfrac {P(D ∩ T)}{P(T)}=\dfrac {0,0784}{0,083} \approx 0,9445,$ soit 0,945 au millième près.
- D’après la question précédente $0,945 < 0,95$. Or, le laboratoire commercialisera le test à partir d'un seuil de $0,95$ donc le test ne sera pas commercialisé.
Partie B
Revoir l’énoncé-
- D’après l’énoncé, la probabilité que l’athlète présente un test positif est $0,103$ quel que soit l’athlète choisi. La variable aléatoire $X$ suit donc une loi binomiale de paramètres $n = 5$ et $p = 0,103$.
- Pour une loi binomiale, on sait que $E = n × p = 5×0,103 = 0,515$.
Ainsi, sur un grand nombre de contrôles, il y aura à peu près $1$ athlète sur $10$ contrôlé positif. -
La probabilité que parmi les 5 athlètes choisis, aucun athlète ne soit contrôlé positif est:
$P(X = 0) = 0,103^0 ×(1−0,103)^5 = 0,8975 \approx 0,5807$ soit environ $0,581$ au millième près.
Donc la probabilité qu’au moins un des 5 athlètes contrôlés présente un test positif est: $1−0,581$, soit $0,419$ au millième près.
-
On a pour n athlètes contrôlés, $P(X = 0) = 0,103^0 ×0,897^n = 0,897^n$.
Il faut donc trouver n tel que :
$1−0,897^n > 0,75 \iff 1−0,75 > 0,897^n \iff 0,25 > 0,897^n$.
La calculatrice donne le plus petit $n \in N$ vérifiant cette inéquation : pour $n = 13$, on a $0,89713 \approx 0,243$.
Il faut donc contrôler 13 athlètes en moyenne pour en trouver un dont le test est positif.
Un biologiste s’intéresse à l’évolution de la population d’une espèce animale sur une île du Pacifique.
Au début de l’année $2020$, cette population comptait $600$ individus. On considère que l’espèce sera menacée d’extinction sur cette île si sa population devient inférieure ou égale à $20$ individus.
Le biologiste modélise le nombre d’individus par la suite $(u_n)$ définie par :
\begin{cases}u_{0} = 0,6\\u_{n+1} = 0,75 u_{n}+(1-0,15u_{n})\end{cases}où pour tout entier naturel $n$, $u_n$ désigne le nombre d’individus, en milliers, au début de l’année $2020+ n$.
Questions
- Estimer, selon ce modèle, le nombre d’individus présents sur l’île au début de l’année $2021$ puis au début de l’année $2022$. Soit $f$ la fonction définie sur l’intervalle $[0; 1]$ par \begin{align}f(x)=0,75x(1−0,15x)\end{align}
- Montrer que la fonction $f$ est croissante sur l’intervalle $[0; 1]$ et dresser son tableau de variations.
- Résoudre dans l’intervalle $[0; 1]$ l’équation $f (x) = x$.
-
- Démontrer par récurrence que pour tout entier naturel $n$, $0 \leq u_{n+1} \leq u_{n} \leq 1$.
- En déduire que la suite $(u_{n})$ est convergente.
- Déterminer la limite $ℓ$ de la suite $(u_{n})$
- Le biologiste a l’intuition que l’espèce sera tôt ou tard menacée d’extinction.
- Justifier que, selon ce modèle, le biologiste a raison.
- Le biologiste a programmé en langage Python la fonction menace() ci-dessous :
On remarquera pour la suite de l’exercice que, pour tout entier naturel $n$, $u_{n+1} = f(u_n)$.
$\qquad u = 0,6$
$\qquad n = 0$
$\qquad$ while $u > 0,02$
$\qquad \qquad u = 0,75*u*(1-0,15*u)$
$\qquad \qquad n = n+1$
$\qquad$ return $n$
Donner la valeur numérique renvoyée lorsqu’on appelle la fonction menace().
Interpréter ce résultat dans le contexte de l’exercice.
-
$2021$ correspond à $n = 1$, donc
$u_{1} = 0,75u_{0} ×(1−0,15u_{0}) $
$=0,75×0,6×(1−0,15× 0,6)$
$ = 0,45×(1−0,09)$
$= 0,45×0,91 $
$= 0,4095$ soit environ $410$ individus.
- $2022$ correspond à $n = 2$, donc
$u_{2} = 0,75u_{1} ×(1−0,15u_{1}) $
$=0,75×0,4095×(1−0,15×0,4095)$
$ = 0,307125×(1−0,061425) $
$= 0,307125×0,938575$
$\approx 0,2282$ soit environ $228$ individus.- $f$ est une fonction polynôme dérivable sur $\mathbb R$, donc sur $[0; 1]$ et sur cet intervalle:
$f'(x) = 0,75(1−0,15x)−0,75x ×0,15 $
$= 0,75−0,1125x −0,1125x $
$= 0,75−0,225x.$
Or $0 \le x \le 1$
$\Rightarrow 0 \le 0,225x \le 0,225 $
$\Rightarrow −0,225 \le −0,225x \le 0$
$\Rightarrow 0,75−0,225 \le 0,75−0,225x \le 0,75 $
ou enfin $0,525 \le f'(x) \le 0,75.$
Sur $[0; 1], f'(x) > 0$, donc $f$ est strictement croissante de \begin{align}f (0) = 0 \text{ à } f (1) = 0,75×0,85 =0,6375.\end{align} - Sur $[0; 1], f (x) = x $
$\iff 0,75x(1 − 0,15x) = x $
$\iff 0,75x(1 − 0,15x)− x = 0 $
$\iff x[0,75(1−0,15x)−1] = 0$
$\iff x(0,75−0,1125x−1) = 0 $
$\iff x(−0,25−0,1125x) = 0 $
\begin{align} \iff \begin{cases} x=0\\ \\ -0,25-0,1125x=0 \end{cases} \text{ ou } \begin{cases} x=0\\ \\ -0,25=0,1125x \end{cases} \text{ ou } \begin{cases} x=0\\ \\ x=-\dfrac{0,25}{0,1125} \end{cases} \end{align}
Dans l’intervalle $[0; 1]$, $0$ la solution unique.
On remarquera pour la suite de l’exercice que, pour tout entier naturel $n, u_{n+1} = f (u_{n})$.
-
-
Initialisation: on a vu que $0 \le 0,4095 \le 0,6 \le 1$, soit $0 \le u1 \le u0 \le 1$ : la relation est vraie au rang $0$.
Hérédité : Supposons que pour $n \in \mathbb N$, on ait:
$0 \le u_{n+1} \le u_{n} \le 1$; la fonction $f$ étant strictement croissante sur $[0; 1],$ on a donc : $f (0) \le f (u_{n+1}) \le f (u_{n}) \le f (1)$,
soit puisque $f (0) = 0$ et $f (1) = 0,75×(1−0,15) = 0,6375 \le 1$ :
$0 \le u_{n+2} \le u_{n+1} \le 1$ : la relation est donc vraie au rang $n +1$.
Conclusion: la relation est vraie au rang $0$ et si elle est vraie au rang $n$ quelconque, elle est vraie au rang $n +1$. Ainsi, d’après le principe de récurrence, pour tout entier naturel $n$, $0 \le u_{n+1} \le u_{n} \le 1$. - D’après la question précédente, la suite $(u_{n})$ est décroissante et minorée par $0$; elle est donc est convergente.
-
Le résultat précédent montre que la suite $(u_{n})$ converge vers un nombre $ℓ \ge 0$
et ce nombre $ℓ$ vérifie l’équation $f (x) = x$.
Or, on a vu à la question 3. qu’elle a $0$ comme solution unique.
On conclut dont que $\lim \limits_{ n \to + \infty }u_{n}=ℓ=0$
-
Initialisation: on a vu que $0 \le 0,4095 \le 0,6 \le 1$, soit $0 \le u1 \le u0 \le 1$ : la relation est vraie au rang $0$.
-
- L’étude précédente a montré que le nombre d’individus décroit, le biologiste a donc raison puisque la limite de la suite du nombre d’individus est égale à zéro.
-
L’algorithme calcule les termes de la suite tant que ceux-ci sont supérieurs à $0,02$. Il s’arrête à $n = 11$ car $u_{10} \approx 0,019$.
L’espèce sera donc menacée d’extinction en $2031$.
Soit $f$ la fonction définie sur l’intervalle $[0; 1]$ par
\begin{align} f (x) = 0,75x(1−0,15x) \end{align}
Les questions 1. à 5. de cet exercice peuvent être traitées de façon indépendante
On considère un cube ABCDEFGH. Le point $I$ est le milieu du segment $[EF]$, le point $J$ est le milieu du segment $[BC]$ et le point $K$ est le milieu du segment $[AE]$.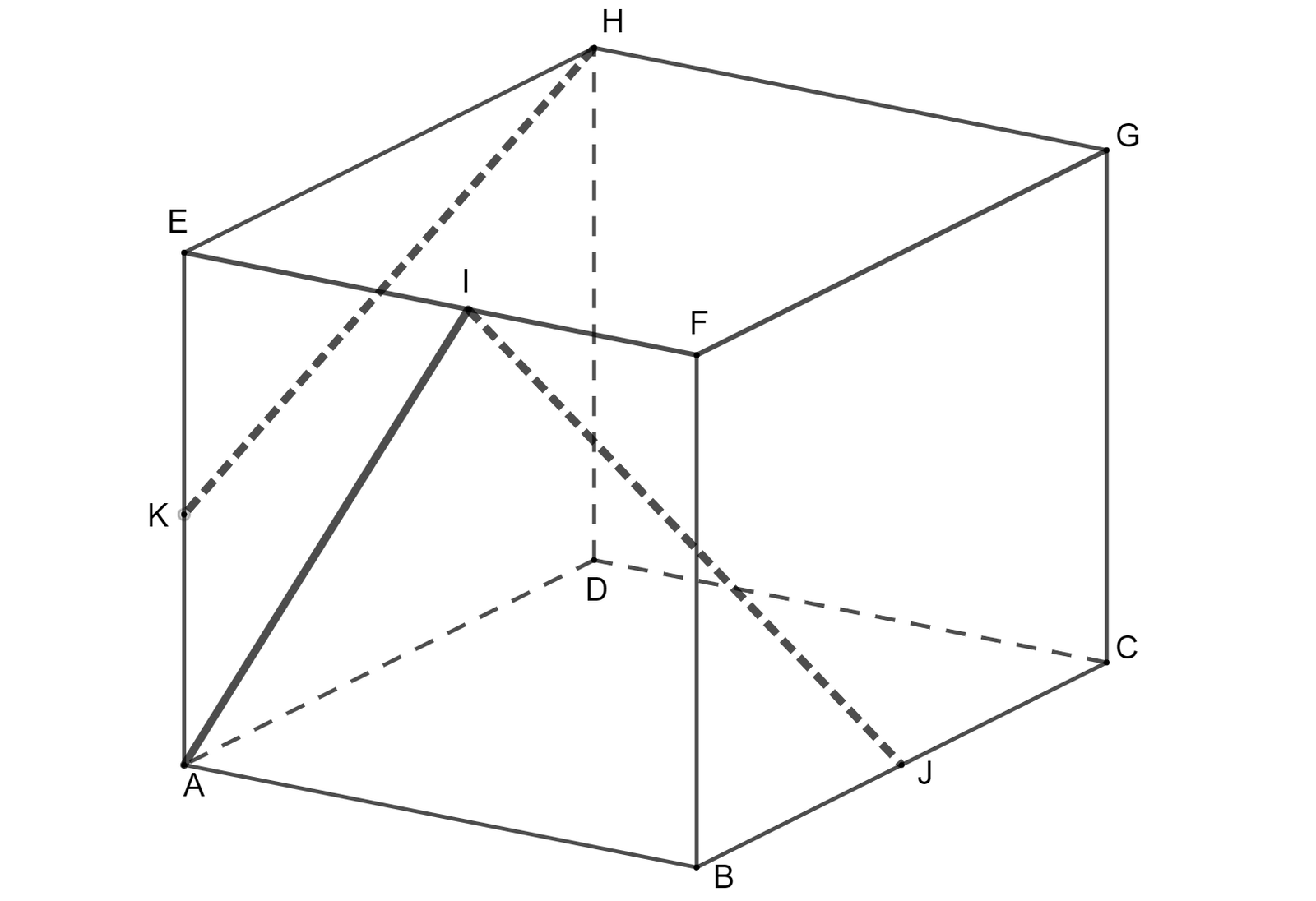
- Les droites $(AI)$ et $(KH)$ sont-elles parallèles? Justifier votre réponse.
Dans la suite, on se place dans le repère orthonormé $(A, \overrightarrow{AB} , \overrightarrow{AD}, \overrightarrow{AE}) $ -
- Donner les coordonnées des points I et J.
- Montrer que les vecteurs $\overrightarrow{IJ}, \overrightarrow{AE}$ et $\overrightarrow{AC}$ sont coplanaires
- Les droites $d_{1}$ et $d_{1}$ sont-elles parallèles? Justifier votre réponse.
- Montrer que la droite $d_2$ est parallèle au plan $P$ .
- Montrer que le point $L(4; 0; 3)$ est le projeté orthogonal du point $M(5; 3; 1)$ sur le plan $P$.
Questions
On considère le plan $P$ d’équation $x +3y −2z +2 = 0$ ainsi que les droites $d_1$ et $d_2$ définies par les représentations paramétriques ci-dessous : \begin{align} d_{1}: \begin{cases} x=3+t\\ \\ y=8-2t\\ \\ z=-2+3t \end{cases} \enspace,t \in \mathbb R \qquad \text{ et } \qquad d_{2}: \begin{cases} x=4+t\\ \\ y=1+t\\ \\ z=8+2t \end{cases} \enspace t \in \mathbb R \end{align}
\begin{cases} A(0 ; 0 ; 0), B(0 ; 0 ; 0), C(1 ; 1 ; 0), D(0 ; 1 ; 0), E(0 ; 0 ; 1) \\ \\ F(1 ; 0 ; 1), G(1 ; 1 ; 1), H(0 ; 1 ; 1), I(0,5 ; 0 ; 1), J(1 ; 0,5 ; 0), K(0 ; 0 ; 0,5) \end{cases}
- On a $\overrightarrow{AI}(0,5 ; 0 ; 1)$ et $\overrightarrow{KH}(0 ; 1 ; 0,5)$: ces vecteurs ne sont pas colinéaires, donc les droites $(AI)$ et $(KH)$ ne sont pas parallèles.
-
- En prenant le repère orthonormé $(A ; \overrightarrow{AB}, \overrightarrow{AD}, \overrightarrow{AE})$ on a:$I(0,5 ; 0 ; 1)$ et $J(1 ; 0,5 ; 0)$
-
On a $\overrightarrow{IJ}(0,5 ; 0,5 ; −1), \overrightarrow{AE}(0 ; 0 ; 1), \overrightarrow{AC}(1 ; 1 ; 0)$.
On a $2\overrightarrow{IJ} +2\overrightarrow{AE} = \overrightarrow{AC}$.
Le vecteur $\overrightarrow{AC}$ est donc une combinaison des vecteurs $\overrightarrow{IJ}$ et $\overrightarrow{AE}$ : ces trois vecteurs sont donc coplanaires.
- $d_1$ a pour vecteur directeur $\overrightarrow{u_1}(1 ; −2 ; 3)$ et $d_2$ a pour vecteur directeur $\overrightarrow{u_2}(1 ; 1 ; 2)$: ces vecteurs ne sont pas colinéaires, donc les droites $d_1$ et $d_2$ ne sont pas parallèles.
-
Le plan a pour vecteur normal le vecteur $\overrightarrow{p} (1 ; 3 ; −2)$ et $d_2$ a pour vecteur directeur $\overrightarrow{u_2}(1 ; 1 ; 2)$.
Or $\overrightarrow{p}.\overrightarrow{u_2} = 1+3−4 = 0$ : les vecteurs sont orthogonaux donc la droite $d_2$ est parallèle au plan $P$.
Soit $∆$ la perpendiculaire à $P$ contenant $M$. Cette droite a pour vecteur directeur le vecteur $\overrightarrow{p}$, donc une équation paramétrique de $∆$ est: \begin{align} \begin{cases} x=5+1t\\ \\ y=3+3t \\ \\ z=1-2t \end{cases} ,t \in \mathbb R \end{align} Le projeté $L$, de $M$ sur le plan $P$ a ses coordonnées qui vérifient les quatre équations: \begin{align} \begin{cases} x=5+1t\\ \\ y=3+3t \\ \\ z=1-2t \\ \\ x+3y-2z+2=0 \end{cases} ,t \in \mathbb R. \end{align} $(5+1t)+3\times (3+3t)-2 \times (1-2t)+2=0 $
$\iff 5+ t +9+9t −2+4t +2 = 0$
$ \iff 14t +14 = 0 \iff t +1 = 0$
$\iff t = −1$.
En reportant dans les trois premières équations du système, on trouve les coordonnées de $L$ projeté orthogonal de M sur $P$ :
\begin{cases} x=5-1\\ \\ y=3+3\times (-1) \\ \\ z=1-2\times (-1) \end{cases} $\iff$ \begin{cases} x=4 \\ \\ y=0 \\ \\ z=3 \end{cases}
Donc le projeté orthogonal de $M$ sur le plan $P$ est le le point $L(4; 0; 3)$.
Méthode 2
On a $\overrightarrow{ML}(−1 ; −3 ; 2)$, donc $\overrightarrow{ML} =- \overrightarrow{p}$ est un vecteur normal au plan $P$.
D’autre part $L(4; 0; 3) \in P \iff 4+3×0−2×3+2 = 6−6 = 0$ est vraie, donc $L$ est le projeté orthogonal de $M$ sur le plan $P$.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On justifiera chaque réponse.
Questions
Affirmation 1: Pour tous réels $a$ et $b$, $(e^{a+b})^2=e^{2a}+e^{2b}$
Affirmation 2: Dans le plan muni d’un repère, la tangente au point A d’abscisse 0 à la courbe représentative de la fonction $f$ définie sur \mathbb{R} par $f (x) = −2+(3− x)e^{x}$ admet pour équation réduite $y = 2x +1$.
Affirmation 3: $\lim \limits_{ x \to +\infty } { e^{2x}-e^{x}+ \dfrac{3}{x}=0 }$
Affirmation 4: L’équation $1−x +e^{-x} = 0$ admet une seule solution appartenant à l’intervalle $[0; 2]$.
Affirmation 5: La fonction $g$ définie sur $\mathbb R$ par $g(x) = x^{2} −5x +e^{x}$ est convexe.
Pour tous réels $a$ et $b$, $(e^{a+b})^2 = e^{2(a+b)} = e^{2a+2b} = e^{2a} \times e^{2b}.$ Donc l’affirmation est fausse.
Affirmation 2:
Une équation de la tangente $t$ au point $A$ d’abscisse $0$ à la courbe représentative de la fonction $f$ définie sur $\mathbb R$ par $f (x) = −2+(3− x)e^x$ est:
$M(x ; y) \in t \iff y − f (0) = f'(0)(x −0).$ Or $f (0) = −2+3e^0 = −2+3 = 1$ et $f'(x) = −e^x +(3− x)e^x = (2− x)e^x$, d’où $f'(0) = 2e^0 = 2$. Donc $M(x ; y) \in t \iff y −1 = 2(x −0) \iff y = 2x +1$. L’affirmation est vraie.
Affirmation 3:
On a quel que soit le réel $x$ : $e^{2x} −e^x + \dfrac{3}{x}=e^x(e^x −1+ \dfrac {3}{xe^x})$. On a $\lim \limits_{ x \to + \infty } xe^x = + \infty,$ donc $\lim \limits_{ x \to + \infty } \dfrac{3}{xe^x}=0.$
Par somme de limites $\lim \limits_{ x \to + \infty }e^x-1+ \dfrac{3}{xe^x}=+ \infty$ et par produit de limites:
$\lim \limits_{ x \to + \infty } e^{x}(e^x-1 + \dfrac {3}{xe^x})=+ \infty$.
L’affirmation est fausse.
Affirmation 4:
Soit la fonction $f$ définie sur $\mathbb R$ par $f (x) = 1− x +e^{−x}$
$f$ est une somme de fonctions dérivables sur $\mathbb R$ donc elle est dérivable et sur cet intervalle:
$f'(x) = −1 − e^{−x} = −(1+e^{−x}) \lt 0$ car quel que soit le réel $x, e^{−x} > 0$, donc $1 + e^{−x} > 1$ puis $−(1+e^{−x}) \lt −1 \lt 0$.
La fonction $f$ est strictement décroissante sur $\mathbb R$.
On a $\lim \limits_{ x \to – \infty } e^{−x} =+ \infty$, et $\lim \limits_{ x \to – \infty } −x =+ \infty$ donc par somme de limites $\lim \limits_{ x \to – \infty }f(x)=+ \infty.$
De même $\lim \limits_{ x \to + \infty } −x =- \infty$ et $\lim \limits_{ x \to + \infty } e^{−x} =0,$ d’où par somme de limites : $\lim \limits_{ x \to + \infty } f(x) =- \infty.$
D’après le théorème des valeurs intermédiaires il existe donc $x_0 \in \mathbb R$ tel que $f (x_0) = 0.$
Comme $f (0) = 1+1 = 2 > 0$ et $f (2) = 1−2+e^2 \approx −0,86 < 0,$ on a bien $0 < x_0 < 2$.
L’affirmation est vraie.
Affirmation 5:
On a $g'(x) = 2x −5+e^x$ et $g”(x) = 2+e^x > 0$
C’est une somme de deux termes supérieurs à zéro, donc $g”(x)>0$ donc la fonction $g$ est donc convexe sur $\mathbb R$.
L’affirmation est vraie.
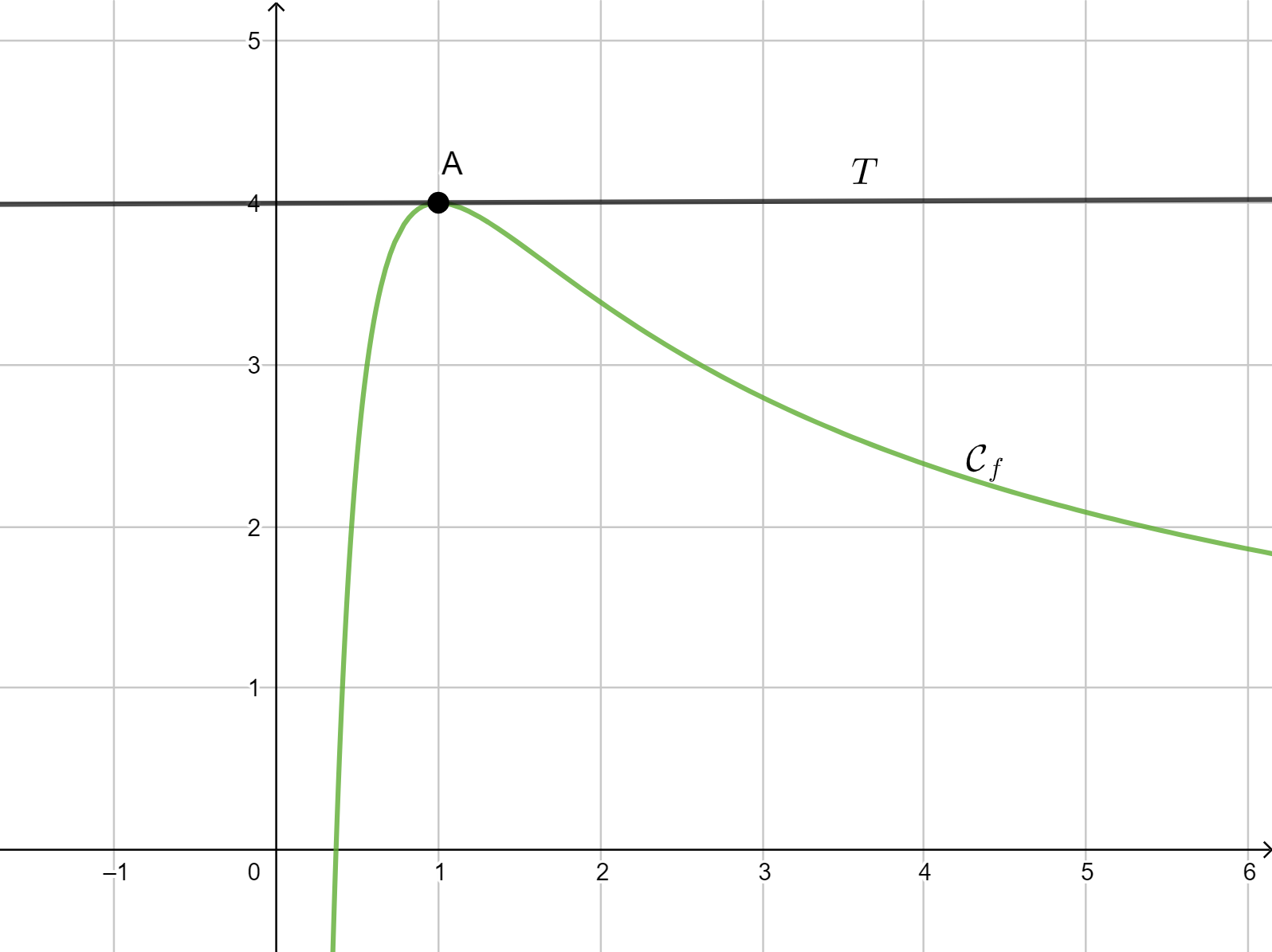
Dans le plan muni d’un repère, on considère ci-dessous la courbe $C_{f}$ représentative d’une fonction $f$, deux fois dérivable sur l’intervalle $]0 ; +\infty[$. La courbe $C_{f}$ admet une tangente horizontale $T$ au point $A(1; 4)$.
Questions
- Préciser les valeurs $f (1)$ et $f'(1)$ On admet que la fonction $f$ est définie pour tout réel $x$ de l’intervalle $]0 ; +\infty[$ par : \begin{align} f(x)=\dfrac{a+b\ln x}{x} \end{align} où $a$ et $b$ sont deux nombres réels.
- Démontrer que, pour tout réel $x$ strictement positif, on a : \begin{align}f'(x)=\dfrac{b-a-b\ln x}{x^{2}}\end{align}
- En déduire les valeurs des réels $a$ et $b$. Dans la suite de l’exercice, on admet que la fonction $f$ est définie pour tout réel $x$ de l’intervalle $]0 ; +\infty[$ par : \begin{align}f(x)=\dfrac{4+4\ln x}{x}\end{align}
- Déterminer les limites de $f$ en $0$ et en $+\infty$.
- Déterminer le tableau de variations de $f$ sur l’intervalle $]0 ; +\infty[$.
- Démontrer que, pour tout réel $x$ strictement positif, on a : \begin{align}f^{”}(x)=\dfrac{-4+8\ln x}{x^{3}}\end{align}
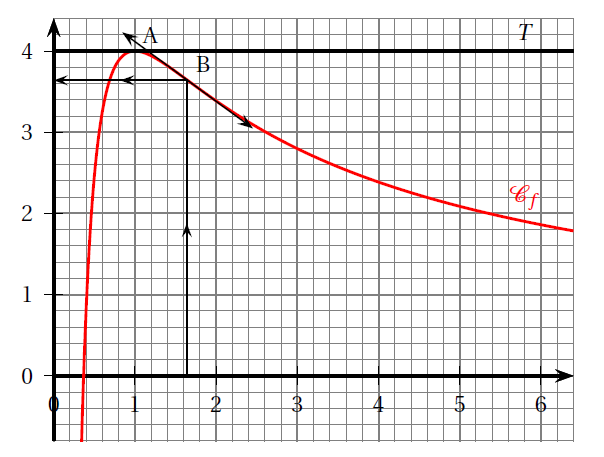
- Montrer que la courbe $C_{f}$ possède un unique point d’inflexion $B$ dont on précisera les coordonnées.
-
$A(1 ; 4) \in C_f$ , donc $f (1) = 4$ et la courbe $C_f$ admet une tangente horizontale $T$ au point $A(1; 4).$ le coefficient directeur de cette tangente en ce point est nul ou encore le nombre dérivé est nul: $f'(1) = 0.$
\begin{align} f(x)=\dfrac{a+b \ln x}{x} \text{ où } a \text{ et } b \text{ sont deux nombres réels.} \end{align} - $f$ est une fonction quotient de fonctions dérivables sur $]0 ; +\infty[,$ le dénominateur ne s’annulant pas et sur cet intervalle: \begin{align} f'(x)=\dfrac{\frac{b}{x}x-1(a+ b\ln x)}{x^2} =\dfrac{b-a-b \ln x}{x^2} \end{align}
- En utilisant les résultats du 1.: \begin{align} f(1)=\dfrac{a+b \ln 1}{1}=4 \iff a=4 \end{align} \begin{align} f'(1)=\dfrac{b-4-b \ln 1}{1^2}=0 \iff b-4=0 \iff b=4 \end{align}
-
-
On sait que $\lim \limits_{ x \to 0 } \dfrac{\ln x}{x}=-\infty;$ donc $\lim \limits_{ x \to 0 } f(x)=-\infty$
On a $f (x) =\dfrac{4}{x}+\dfrac{4 \ln x}{x}$ On a $\lim \limits_{ x \to +\infty }=\dfrac{4}{x}=0$ et on sait que $\lim \limits_{ x \to +\infty }=\dfrac{4\ln x}{x}=0$ donc par somme de limites:
$\lim \limits_{ x \to +\infty }f(x)=0$ -
On a donc sur $]0 ; +\infty[, f'(x) =\dfrac{−4\ln x}{x}$ qui a pour signe celui de $−4\ln x$.
On sait que sur $]0 ; 1[, \ln x < 0$, donc $f'(x) > 0$ sur $]0; 1[;$
Par contre sur $]1 ; +∞[, \ln x > 0$, donc $f'(x) < 0$ sur $]1 ; +\infty[$;
$f'(1) = 0$, donc le point de coordonnées $(1; 4)$ est le maximum de la fonction sur $]1 ; +\infty[.$
La fonction $f$ est donc croissante sur $]0; 1[$ de $-\infty$ à $4$, puis décroissante sur $]1 ; +\infty[$ de $4$ à $0$ avec un maximum $4$ pour $x = 1$. - $f’$ étant une fonction quotient de fonctions dérivables sur $]0 ; +\infty[$, le dénominateur ne s’annulant pas est dérivable et sur cet intervalle: $f”(x)=\dfrac{-4\times \frac{1}{x}\times x^2-2x\times (-4\ln x)}{x^4}=\dfrac{-4x+8x\ln x}{x^4}=\dfrac{-4+8\ln x}{x^3}$
-
La courbe présente un point d’inflexion lorsque la dérivée seconde s’annule.
Or: $f”(x)=0 \iff \dfrac{-4+8\ln x}{x^3}=0 \iff -4+8\ln x=0 \iff -1+2\ln x=0 \iff$
$\ln x =\dfrac{1}{2} \iff x = e^ {\frac{1}{2}} \approx 1,649(\text{ ou } \sqrt e$.
L’ordonnée de ce point unique d’inflexion est $f(e^{\frac{1}{2}})=\dfrac{4+4\times \frac{1}{2}}{e^\frac{1}{2}}=$
$\dfrac{6}{e^ {\frac{1}{2}}}=\dfrac{6}{\sqrt e} \approx 3,639.$
Ce point d’inflexion et la tangente en ce point sont indiqués sur la figure ci-dessous.
Dans la suite de l’exercice, on admet que la fonction $f$ est définie pour tout réel $x$ de l’intervalle $]0 ; +\infty[$ par: \begin{align} f(x)=\dfrac{4+4 \ln x}{x} \end{align}