Quiz et exercices : Espérance, variance, écart-type
Exercice 1 (niveau 1) :
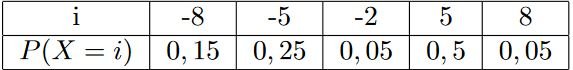
Calculer l’espérance, la variance, et l’écart-type de la variable aléatoire associée à cette loi.
En appliquant les formules de cours, on a :
$E(X) = (-8) \times 0,15 + (-5) \times 0,25 + (-2) \times 0,05 + 5 \times 0,5 + 8 \times 0,05 = 0,35$
$V(X) = 31,6275$
$\sigma(X) = \sqrt{V(X)} = 5,62$
Exercice 2 (niveau 1) :
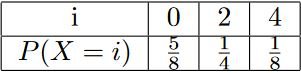
Calculer l’espérance, la variance, et l’écart-type de la variable aléatoire associée à cette loi.
En appliquant les formules de cours, on a :
$E(X) = 0 \times \frac{5}{8} + 2 \times \frac{1}{4} + 4 \times \frac{1}{8} = 1$
$V(X) = \frac{5}{8} \times (0 – 1)^2 + \frac{1}{4} \times (2-1)^2 + \frac{1}{8} \times (4-1)^2 = \frac{3}{4}$
$\sigma(X) = \sqrt{V(X)} = \frac{\sqrt{3}}{2}$
Exercice 3 (niveau 2) :
Soit X une variable aléatoire dont on donne dans le tableau suivant sa loi de probabilité :
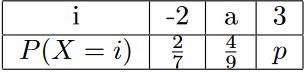
- Que vaut p ?
- Que vaut a pour qu’on ai $E(X) = 2$ ?
1. La somme des probabilités doit faire 1, donc $p + \frac{2}{7} + \frac{4}{9} = 1$ d’où $p = 1 – \frac{2}{7} – \frac{4}{9} = \frac{17}{63}$.
2. On a $E(X) = -2 \times \frac{2}{7} + a \times \frac{4}{9} + 3 \times \frac{17}{63}$. On cherche donc à résoudre l’équation $-2 \times \frac{2}{7} + a \times \frac{4}{9} + 3 \times \frac{17}{63} = 2$ d’inconnue $a$. On trouve $a = – \frac{15}{28}$.
Exercice 4 (niveau 3) :
Après avoir misé une certaine somme d’argent, un joueur lance un dé à six faces. Il gagne 3 € et sa mise s’il n’obtient pas un diviseur de 6, il perd sa mise sinon. Quel doit être le montant de la mise pour que le jeu soit équitable (c’est-à-dire pour que l’espérance de gain soit nulle) ?
On note $a$ la mise du joueur. On a donc deux issues possibles, soit le joueur gagne $a+3$ euros, soit il perd $a$ euros. Donc $\Omega = {-a, a+3}$ et on a :
$P(X = a + 3) = \frac{1}{3}$ (car seuls $4$ et $5$ ne divisent pas $6$ donc, $2$ chances sur $6$ soit une chance sur $3$)
$P(X = -a) = \frac{2}{3}$
Et $E(X) = -a \times \frac{2}{3} + (a+3) \times \frac{1}{3}$. On cherche à avoir $E(X) = 0$ donc à résoudre l’équation $-a \times \frac{2}{3} + (a+3) \times \frac{1}{3} = 0$ d’inconnue $a$. On obtient $a = 3$.
